Exercice 1 : Des polygones.
On représente des polygones par des listes de sommets.
type point = (float * float)
type polygon = point list
Écrivez une fonction qui étant donné un polygone, retourne le point d'abscisse minimale de ce polygone (on peut utiliser le flottant infinity).
Écrivez une fonction qui étant donnée une liste de polygones, retourne le point d'abscisse minimale parmi tous les polygones.
Écrivez une fonction qui calcule les coordonnées du plus petit rectangle parallèle aux axes, contenant tous les polygones de la liste.
Exercice 2 : Distance d'édition.
On nous donne les fonctions suivantes :
val levenshtein : string -> string -> int
val jaccard : string -> string -> float
Écrivez une fonction qui à un mot target : string et une liste de mots words : string list, calcule les mots parmi words à distance de Levensthein de 3 ou moins de word, triés par distance croissante. On ne doit calculer la distance de Levenshtein d'une paire de mots qu'au plus une fois.
Modifiez la solution pour supprimer dans un premier temps tous les mots dont la distance de Jaccard à target est au moins
.
Exercice 3 : Égalité de listes.
Écrivez une fonction d'égalité de listes, prenant en argument le prédicat d'égalité des éléments. On peut utiliser List.zip.
val are_equals :
equals:('elt -> 'elt -> bool)
-> 'elt list -> 'elt list -> bool
Exercice 4 : Palindrome
Donnez une fonction vérifiant si une liste est un palindrome. La liste
est un palindrome si pour tout
.
Exercice 5 : Tri rapide
Écrivez une fonction smaller qui prend un entier et une liste d'entier , et calcule la sous-liste des entiers de plus petits que ou égaux à .
Ajoutez une fonction bigger, qui renvoie cette fois la liste des éléments strictement plus grand que .
En déduire l'algorithme de tri rapide.
bigger et smaller nous obligent à faire deux parcours de la liste à chaque appel récursif. Utilisez fold_left pour calculer en même temps les deux listes : celle des éléments plus petits et celle des éléments plus grand.
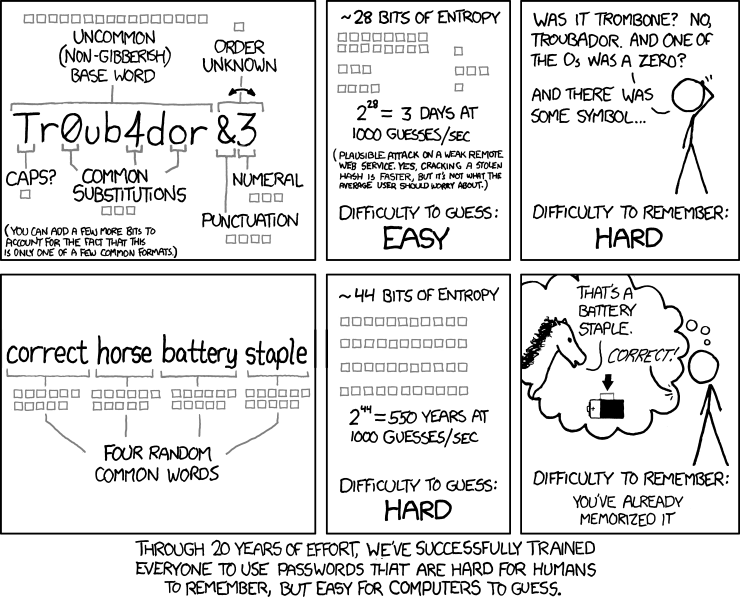
Exercice 6 : génération de mots de passe.
(sources: xkcd.com)
On souhaite générer un mot de passe en tirant mots aléatoirements dans un dictionnaire, en les capitalisant et en les concaténant. On dispose de :
val dictionary : string list
val k : int
val Random.int : int -> int
val String.concat : string list -> string
val String.capitalize : string -> string
Utiliser les fonctions de listes pour écrire le générateur de mots de passe.
Exercice 7 : Triplets Pythagoriciens
Comment calculer la liste de tous les triplets pythagoriciens
avec d'entiers inférieurs à 100 , en utilisant map, filter et concat ? Il faudra aussi utiliser la fonction range déjà vue plusieurs fois.
Exercice 8 : Rendu de monnaie
Soit une quantité de monnaie en centimes. Donnez un algorithme qui produit la liste de toutes les façons de payer . Par exemple, une façon de rendre 243 centimes est d'utiliser deux pièces de 1 € , deux pièces de 20 ¢ , et trois pièces de 1 ¢ . On considère que le nombre de pièces disponibles est illimité. On pourra commencer en considérant seulement des pièces de 5 ¢ , 2 ¢ et 1 ¢ .
Généralisez l'algorithme pour qu'il prenne en argument la liste des monnaies disponibles.
Exercice 9 : Problème des -reines
On souhaite trouver les solutions du problème des -reines : placer
reines sur un échiquier de dimension , sans qu'aucune ne soit menacée par une autre.
type position = (int * int)
Donnez une fonction are_not_threatening : position ->
position -> bool vérifiant que deux reines ne se menacent pas.
Étendez cette fonction en is_not_threatened : position list
-> position -> bool, vérifiant qu'une reine n'est pas menacée par une des reines déjà placées.
Écrivez une fonction board : int -> position list créant la liste des cases de l'échiquier, pour une dimension donnée.
Donnez une fonction énumérant les solutions du problème des
-reines.