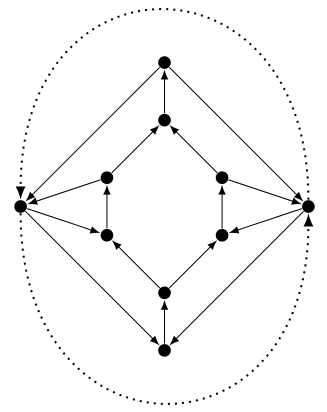
The round-trip problem is a special case of the arc-disjoint paths problem in planar graphs, when we have only two commodities $(s,t), (t,s)$. In other words, we want to decide whether there is a directed cycle (not necessarily simple), containing both $s$ and $t$.
It is known to be np-complete in non-planar graphs, but still open in general graphs. Here is an example showing a graph with a fractional solution but no integral solution.
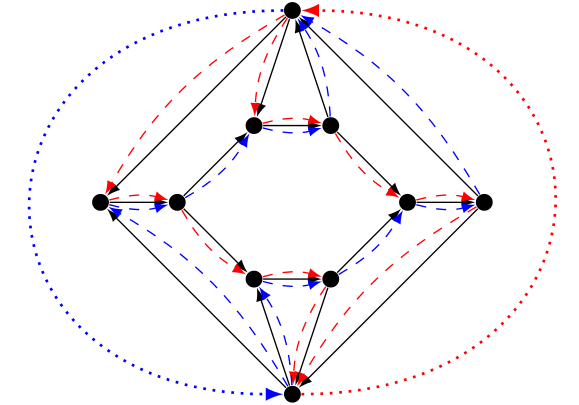
There are two demands, figured by dotted arcs. Each demand is satisfied by taking the two paths of its color, with value half.
This is one of the open problems listed in Lex Schrijver's book.