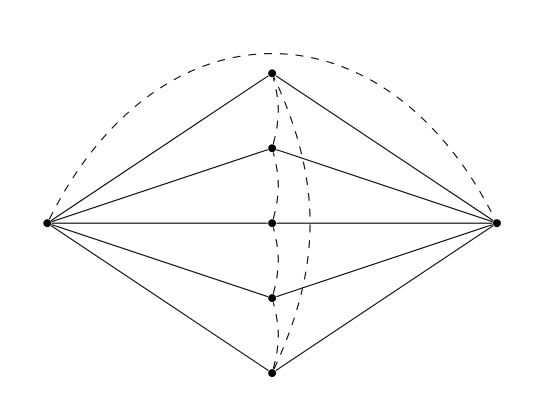
The main result in the same paper by Chakrabarty, Fleischer and Weibel [1] characterizes the pairs $(G,H)$, with $G$ a series-parallel graph, for which there is an integral routing for any $c,D$ satisfying the cut condition. Let $K_{n,p}$ be the complete bipartite graph with parts of cardinals $n$ and $p$. We call odd-spindle a pair $G,H$ with $G = K_{2,m}$ with $m \geq 3$ even, and $H$ is composed of a simple cycle of length $m$ spanning the vertices of degree $2$ of $G$, plus an edge between the two vertices of degree $m$. For $m=5$, it gives:
A minor of a pair $G,H$ is a pair $G',H'$ obtained from $G,H$ by a sequence of contraction of edges of $G$ and deletion of edges of $G$ and $H$.
A graph $G$ is series-parallel ($G$ is a SP graph) if it can be obtained from an arbitrary tree by a sequence of series and parallel operation. A series operation replace an edge by a path of arbitrarily length, with the same endpoints and all the inner vertices are fresh vertices. A parallel operation replicates an edge in an arbitrary number of edges with the same endpoints. Series-parallel graphs coincides with graphs with no minor $K_4$, and with graphs of tree-width $2$.
A pair $G,H$ is cut-sufficient if for any $c,D$ such that any instance $G,H,c,D$ that satisfies the cut condition admits a (fractional) solution.
Theorem 1: (Chakrabarty , Fleischer and Weibel [1]) If $G$ is series-parallel, then $G,H$ is cut-sufficient if and only if $(G,H)$ has no odd-spindle minors. If $G,H,c,d$ is Eulerian and satifies the cut condition, then there is an integral solution.
The proof relies on the congestion-distortion equivalence theorem, and a particular case of cut-sufficiency for $G$ series-parallel that was proved in an earlier paper by Chekuri, Shepherd and Weibel [2]. One implication is clear: an odd-spindle with $c$ and $D$ uniformly equal to $1$ is cut-sufficient, though there is no solution. As being cut-sufficient is obviously closed under the minor operations, the cut-sufficiency implies that there is no odd-spindle minor.
Let $G,H,c,D$ be an instance that satifies the cut condition. We may assume that:
Series-parallel graphs have very strong structural properties. As mentionned above, they are graphs of treewidth 2 , which implies that there are many 2-vertex-cuts. Let's take an arbitrary 2-vertex-cut $\{u,v\}$, and consider the graph obtained by contracting all the edges of $G \setminus \{u,v\}$: this graph is a $K_{2,m}$. We start by proving the following. A $K_{2,m}$-instance is an instance $G,H$ where $G$ is a $K_{2,m}$ with possibly one additional edge between the two vertices of degree $m$.
Lemma 2: (Chekuri , Shepherd, Weibel [2]) if $G,H$ is a $K_{2,m}$-instance and $G,H$ does not have an odd-spindle as a minor, then $G,H$ is cut-sufficient.
Proof: Recall that $\sigma(X)$ denotes the surplus of the cut defined by $X$.
Let $c,D$ satisfy the cut condition. We denote by $s,t$ the two vertices of degree $m$, and $U = \{u_1,\ldots,u_m\}$ the vertices of degree $2$ in $G$. By assumption $\delta(U,\{s,t\}) = \emptyset$. We may also assume that $\delta(u_i)$ is tight for any $u_i$, otherwise we increase the capacity on the edge $st$ and decrease it on $\delta_G(u_i)$. Then simplify the instance by removing parallel edges in $G$ and $H$.
Lemma 3: If $H[U]$ is bipartite, then $G,H$ is cut-sufficient.
Proof: $H[U]$ is bipartite, with parts $X \cup Y = U$. Let $xy$ be a demand with $x \in X$, $y \in Y$. We would like to do one of the following operation without violating the cut-condition:
If the first one can't be done, there is a central tight cut $S$containing $s$ but not $x$ and $y$. If the second one can't be done there is a central tight cut $T$ containing $x$ and $y$ but not $t$.
We partition $X \cup Y$ into parts $A$ to $H$ as in the next figure, where $S$ is the red set, $T$ the blue set. For instance $A = X \cap S \cap T$, $H = Y \cap T \setminus X$, and $x \in G$, $y \in H$.
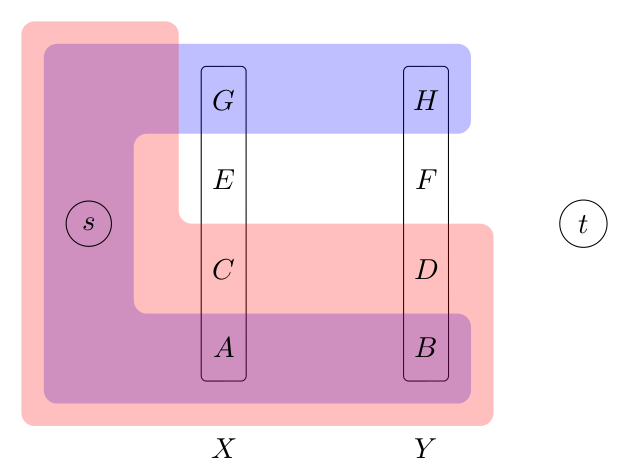
Let $S' = \{s\} \cup A \cup B \cup C \cup G$ and $T' = \{s\} \cup A \cup B \cup D \cup H$. Then, by counting (and remembering that $X,Y$ is a bipartition for $H[U]$ and $U$ is independant in $G$):
$$0 = \sigma(S) + \sigma(T) = \sigma(S') + \sigma(T') - \sigma(C,D) - \sigma(G,H) + \sigma(C,G) + \sigma(D,H)$$
Because $\sigma(S') \geq 0$ and $\sigma(T') \geq 0$ (cut condition):
$$ 0 \leq \sigma(S') + \sigma(T') = \sigma(C,D) + \sigma(G,H) = - D(\delta_H[C,D] \cup \delta_H[G,H]) < 0$$
The last inequality comes from the existence of the demand $xy$. This is a contradiction, hence one of the two operations can be carried out. Also, these operations preserves the integrality of the surplus function, hence at least $1/2$ of the demand can be moved this way at each step. By induction upon the total demand, we reduce the instance to an instance with demand only between $st$, where the cut condition is sufficient.
Suppose $D_{st} > 0$. Then, as $\delta(\{u\})$ is tight for any $u \in U$, the instance is not feasible, hence $H[U]$ is not bipartite. We get an odd cycle in $H[U]$ and so an odd-spindle minor in $G+H$.
Suppose now that $D_{st} = 0$. Then we try to choose for any demand edge $uv$, how much of $D_{uv}$ is routed along the path $usv$, with respect to using exactly all of the capacities of $\delta_G(s) - \{st\}$. This is a capacitated fractional $b$-matching problem on vertices $U + z$ and edges $H[U] \cup \{zu, u \in U\}$ with $b(v) = c(sv)$, and where $z$ is an dummy vertex with $b(z) = c(st)$ and $z$ is adjacent to every node (including itself) in $U$ with infinite capacity. If a solution exists then we easily deduce a solution to the routing problem. Otherwise we know that there exists three sets $S \ni z$, $N$ and $W$ partitioning $U \cup \{z\}$, with:
$$ 2D(\delta_H[N]) + D(\delta_H[N,W]) < c(\delta_G(N,\{s\})) - c(\delta_G(S,\{s\}))$$
Because each vertex in $N$ defines a tight set we also have:
$$ 2D(\delta_H[N]) + D(\delta_H[N,S]) + D(\delta_H[N,W]) = c(\delta_G(N,\{s\})) + c(\delta_G(N,\{t\}))$$
Subtracting it from the inequality, we get:
$$ \varepsilon = D(\delta_H[N,S]) - c(\delta_G(S,\{s\})) - c(\delta_G(N,\{t\})) > 0$$
Consider the instance $G',H'$ obtained from $G[\{s,t\} \cup W], H[W]$ by adding a demand edge $st$ with $D_{st} = \varepsilon$. If there is a cut $X \ni t$ with negative excess in $G',H'$, then $X \cup S$ is a cut with negative excess in $G,H$, contradiction. But the instance is not feasible: $\delta(w)$ is tight for each $w\in W$ so the demand $st$ cannot be routed through $W$. Hence by induction $G',H'$ contains an odd-spindle as a minor, from which we get that $G,H$ contains an odd-spindle too, using a demand edge in $\delta_H[S,N]$.
We recall some properties of series-parallel graphs. Remember that a SP graph is a graph with no minor $K_4$.
Lemma 4: In a SP graph, a simple cycle does not intersect any central cut more than twice.
Proof: By contradiction.
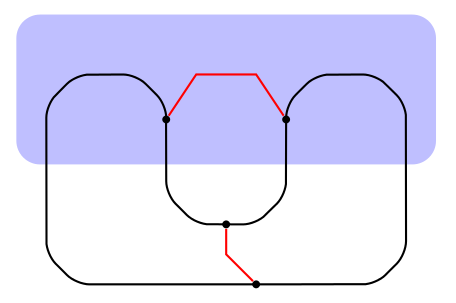
Use the centrality of the cut to get the red paths, this gives a $K_4$ minor.
Lemma 5: In a SP graph, if there are three node-disjoint $(u,v)$-paths, then $\{u,v\}$ is a $2$-cut.
Proof: Any path between the inner nodes of two distinct $(u,v)$ paths would give a $K_4$.
Lemma 6: Let $u$, $v$ be a pair of nodes, $l$ and $r$ be a $2$-cut separating $u$ from $v$, $L$, $R$ two central sets with $l \in L, r,u,v \notin L$ and $r \in R, u, l, v \notin R$. Then $L \setminus R$, $R \setminus L$ are central.
Proof: $V \setminus (R \setminus L)$ is connected as $V \setminus R$ and $L$ are connected and intersect in $l$. It remains to prove that $R \setminus L$ is connected. By contradiction.
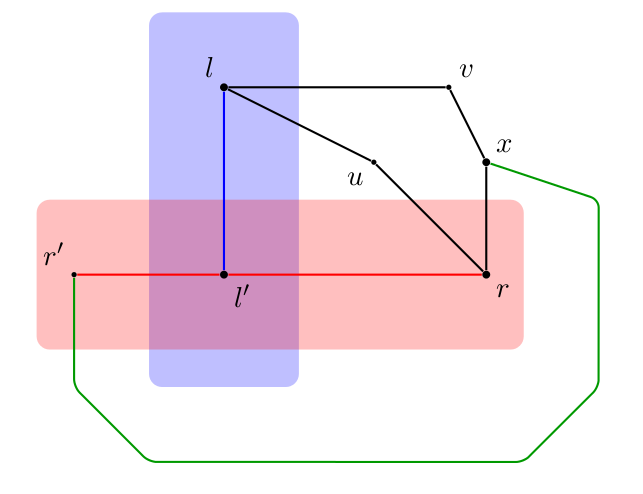
First case : suppose $r'$ is disconnected from $r$, with $r'$ in the component of $v$ in $G[V \setminus \{l,r\}]$. Then take the red path by centrality of $R$, the blue path by centrality of $B$, the green path by centrality of $L$ (to get to $V \setminus (R \cup L)$) and $R$ (then to $u$ or $v$). $x, l, l', r$ give a $K_4$.
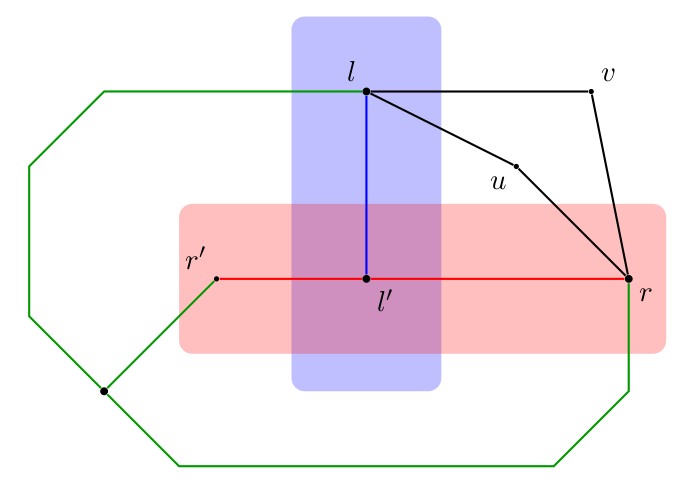
Second case : suppose $r'$ is disconnected from $r$, with $r'$ not in the component of $u$ or $v$ in $G[V \setminus \{l,r\}]$. Then again take the red and blue path, then the green to $V \setminus (R \cup L)$, then use the centrality of $L$ and $R$ to complete the green path to somewhere (in $L \setminus R$) between $l'$ and $l$ and somewhere (in $R \setminus L$) between $l'$ and $r$. this gives a $K_4$.
Lemma 7: For any $2$-cut $\{u,v\}$ in a SP graph $G$ and any component $C$ of $G \setminus \{u,v\}$, there is a vertex $w$ (not necessarily unique) such that $G[C \cup \{w\}]$ is disconnected.
Proof: By contradiction. We immediately get a $K_4$.
Lemma 8: Given any $2$-cut $\{s,t\}$ in a SP graph $G$, there is a unique acyclic orientation of $E(G)$ with $s$ being the unique source and $t$ the unique sink.
Proof: By recursion, using the previous lemma.
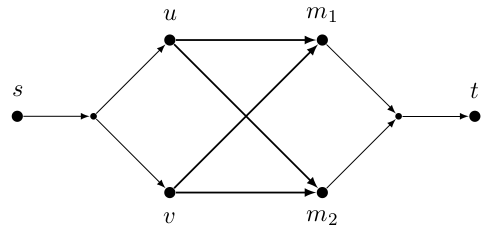
Lemma 9: Orient a SP graph $G$ with respect to a $2$-cut $\{s,t\}$. Define the relation $u \preceq v$ if there is a directed path from $u$ to $v$. Then $\preceq$ defines a lattice.
Proof: By contradiction. Let $u,v$ be a maximal pair such that there are $m_1$ and $m_2$ with $u,v \preceq m_1, m2$ but $m_1$ and $m_2$ are not comparable. Then there is a $K_4$.
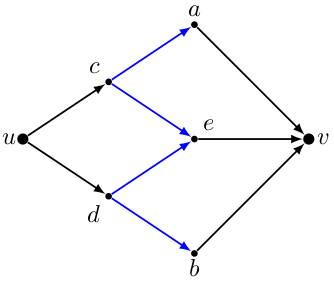
Lemma 10: Given the acyclic orientation induced by a $2$-cut $\{s,t\}$ in a SP graph $G$, any simple cycle can be decomposed into two directed $\{u,v\}$-paths. Then $\{u,v\}$ is a $2$-cut.
Proof: By contradiction. Take four maximal consecutive directive paths on a simple cycle $C$. Get $v$ as $a \lor b$ and $u$ as $c \land d$. If $e \neq v$ we get a $K_4$, hence $a,b \preceq e = v$. Repeat on all the possible way to choose the four blue paths, we eventually get that $a = b = e$, this contradicts the simplicity of $C$.
We prove the second statement. if $\{u,v\} = \{s,t\}$ it is a $2$-cut. Else there are directed paths from $s$ to $u$, from $s$ to $t$ and from $v$ to $t$. Together they define a third disjoint $(u,v)$-path. Hence $\{u,v\}$ is a $2$-cut.
We say that an edge $e \in H$ is fully compliant if $G+e$ is series-parallel, and that an instance is fully compliant if every demand edge is compliant. The proof of the cut-sufficiency condition for fully compliant instances relies on a $2$-cut reduction that we now describe. Suppose there is a $2$-cut $\{u,v\}$, and a partition $A$, $B$ of the components of $G \setminus \{u,v\}$, such that $\delta_H\left[V(A),V(B)\right] = \emptyset$. Then we can reduce the problem into two instances over $A \cup \{s,t\}$ and $B \cup \{s,t\}$respectively. We may have to add a demand edge $st$ in one of them, and a supply edge $st$ in the other, in order to make the two instances satisfy the cut condition, but there is no difficulty in doing so and proving the correctness of this reduction.
Now it is easy to prove that fully compliant instances are cut-sufficient. We may assume that there is a 2-cut $\{u,v\}$ with three disjoint $(u,v)$-paths, otherwise $G$ is a simple cycle for which cut-sufficiency is well-known (for example by Okamura-Seymour's theorem). As $\{u,v\}$ is a vertex cut there is a partition $A,B$ of $V \setminus \{u,v\}$, with $\delta_G[A,B] = \emptyset$, and we can assume not all the three paths are in one side. Now, $\delta_H[A,B] = \emptyset$, otherwise we could find a path connecting two of our three $(u,v)$-paths, and this would give a $K_4$ minor. Hence we can apply the $2$-cut reduction. This gives:
Lemma 11: (Chekuri , Shepherd, Weibel [2]) Fully compliant instances are cut-sufficient.
Choose any $2$-cut $st$ and consider the associated acyclic orientation. Say that an edge $uv$ is compliant (for this orientation) if there is a directed $(s,t)$-path containing $u$ and $v$. An instance is compliant if there is an acyclic orientation for some $2$-cut $\{s,t\}$ such that every demand edge is compliant or fully compliant (it may happen that a fully compliant edge is not compliant, if there are no three node-disjoint $(s,t)$-paths). The next step is:
Lemma 12: (Chekuri , Shepherd, Weibel [2]) Compliant instances are cut-sufficient.
Proof: If all the demand edges are fully compliant we are done. Hence we can assume that there is a demand edge $uv$ that is not fully compliant, but only compliant. Our goal is to replace $uv$ by two demand edges $uw,wv$ such that the new instance is still compliant, satisfies the cut condition and is somehow simpler.
Lemma 13: If an edge $uv$ is not fully compliant, then there is a $2$-cut $\{l,r\}$ separating $u$ from $v$, and three disjoint paths from $l$ to $r$.
Proof: $G+uv$ has a $K_4$ minor, containing the edge $uv$, hence there are $a,b,c,d$ vertices and $6$ paths joining every possible pairs, one of them containing $uv$, say the $(a,b)$-path $P_{ab}$. Then by removing $P_{ab}$, we get three disjoint $(c,d)$-paths. Hence $\{c,d\}$ is the $2$-cut that we are looking for.
Because $uv$ is compliant there is a directed $(s,t)$-path $P$ going through $s,u,v,t$ in that order. Because $u,v$ is not fully compliant there is two cut $l,r$ separating $u$ from $v$, and three disjoint $(r,l)$-paths. We may choose one of them to contain an $s't'$ path $Q$. We may assume that $r$ is on $P$ between $u$ and $v$. $l$ must be in the same component as $u$ and $v$ in $G \setminus \{s,t\}$, because one of the three $(l,r)$-paths does not contain $s$ or $t$ (and $\{s,t\}$ is a $2$-cut). $l,r$ separates $u$ from $v$, hence $l$ is on $P$, between $s$ and $u$ or between $v$ and $t$. Let's say $P$ goes through $s,l,u,r,v,t$ in that order.
We want to replace the demand edge $uv$ by two demand edges $ul,lv$ or $ur,rv$. Suppose this is not possible, and we will derive a contradiction. Then we get two central tight cuts $L$ and $R$ where:
$L$ and $R$ are central, so are $L \setminus R$ and $R \setminus L$ by Lemma 6. Consider $G \setminus (L \bigtriangleup R)$ and its components $C_i$, $u$ and $v$ are in two distinct components (as $\{l,r\}$ separates them). Suppose some component $C_j$ has two vertices $x,y$ with $x \in L \cup R$ and $y \in $V \ setminus $L \cup R)$. $L$ and $R$ are connected, hence there are two paths from $x$, one to $L \setminus R$, one to $R \setminus L$. $V \setminus L$ and $V \setminus R$ are also connected, hence there are two paths from $y$ to $L \setminus R$ and from $y$ to $R \setminus L$. These four paths can be chosen node-disjoint. Moreover, there is an $(x,y)$-path in $C_j$ and a $(L \setminus R,R \setminus L)$-path avoiding $C_j$. This gives a $K_4$. Hence each $C_i$ is completely contained in either $L \cap R$ or $V \setminus (L \cup R)$.
As the cycle $C = P \cup Q$ intersects $\delta(R)$and $\delta(S)$ exactly twice each, we have:
Suppose first that $t$ is in the same component $C_v$ as $v$. Then take any demand edge $ab$, and consider a directed $(s,t)$-path $P'$ containing $a$ and $b$ (because $ab$ is compliant). If $a$ and $b$ are in two distinct components, and distinct from the component $C_v$, then $P'$ intersects at least 5 times $\delta(L \setminus R)$ and $\delta(R \setminus L)$, contradiction. Any demand between two components has one endpoint in $C_v$.
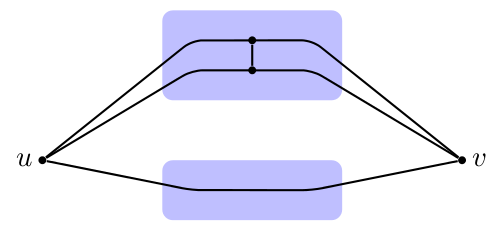
Suppose now that $s, t \in L \setminus R$. Take a component $C_i$ of $G[V \setminus (L \bigtriangleup R)]$, and suppose that $\delta^+(C,R \setminus L)$ and $\delta^-(C,R \setminus L)$ are both non-empty, then there is $e^+$ and $e^-$ as evidence. $e^+$ is in some path $P^+$ starting from $s$ and $e^-$ is in some path $P^-$ ending at $t$ (by the acyclic orientation of $G$). Because $\delta(R \setminus L)$ and $\delta(L \setminus R)$ can be crossed at most twice by a cycle, the situation looks like the following picture:
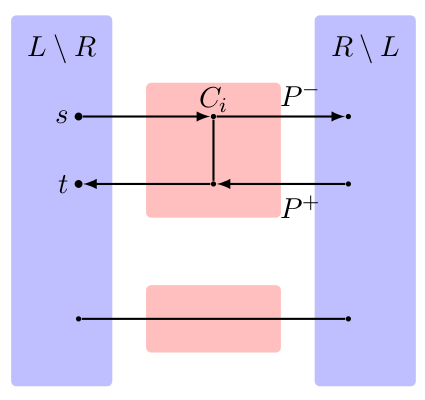
$P^-$ and $P^+$ are vertex-disjoint: otherwise we could make a directed path from $R \setminus L$ to itself through $C_i$. This path could then be extended into an $(s,t)$-path crossing $\delta(R \setminus L)$ four times, contradiction. $C_i$ is connected hence there is a path between a node $x$ of $V(P^+ \cap C_i)$ and a node $y$ of $V(P^- \cap C_i)$, in $C_i$. Using another component $C_j$ (there are at least two components, and each of them is connected to $L \setminus R$ and $R \setminus L$ by centrality of these sets), and the connectedness of $L \setminus R$ and $R \setminus L$, we get a $K_4$.
From this we conclude that every component $C_i$ has $\delta^+(C_i,R \setminus L) = \emptyset$ (out-component) or $\delta^-(C_i,R \setminus L) = \emptyset$ (in-component). Moreover any demand edge $ab$ between two components is contained in an $(s,t)$-path which crosses $\delta(L \setminus R)$ and $\delta(R \setminus L)$ exactly twice, hence $a$ is in an out-component and $b$ is in an in-component.
Hence, in both cases, the instance obtained by contracting each component into a single node, as well as $L \setminus R$ and $R \setminus L$ is a $K_{2,m}$ with $H[U]$ bipartite where $U$ is the set of vertices of degree $2$. Moreover the new instance satisfies the cut condition (we only did minor operations), but the cut induced by $\delta(L)$ and $\delta(R)$ in the contracted graph are tight and show that no routing may exists. This contradicts the simultaneous existence of $L$ and $R$.
Thus, the demand $uv$ can be pushed to either $r$ or $l$. Then the number of compliant but not fully compliant demand edges is decreased by one. By induction the instance is routable.
We now give a proof of the general theorem 1 for series-parallel graphs: $G,H$ is cut-sufficient if and only if it does not contain an odd-spindle minor. We only proved on direction, let's prove the other one: we assume that $G,H$ is not cut-sufficient (that is $G,H$ has congestion greater than $1$) and prove that it contains an odd-spindle.
We start with a consequence of the congestion-distortion equivalence, that can be proved by carefully applying the complementarity slackness conditions in the proof of the congestion-distortion equivalence. Given capacities $c$, demands $D$ and a demand edge $uv$, we say that a set $W$ is a bubble for $uv$ is $\delta(W)$ is tight and $u,v \notin W$. We say that the set $\mathcal{P}_{uv}$ of $(u,v)$-paths is covered by bubbles if every path in it intersects at least one bubble for $uv$. Then we use the following fact (that we don't prove):
Lemma 14: If $G,H$ is not sufficient, then there are $c$ and $D$ such that for any demand edge $uv$, if $P \in \mathcal{P}_{uv}$ does not cross any bubble, then $P$ crosses some tight cut more than once. ($c$ and $D$ can actually be taken to be optimal solutions for the maximization of congestion problem).
We take $c$ and $D$ as in the lemma. Now the proof is in two parts: finding a demand $uv$ with $\mathcal{P}_{uv}$ covered by bubbles, and from there finding an odd-spindle.
Lemma 15: There is a demand edge $uv$ such that $\mathcal{P}_{uv}$ is covered by bubbles.
Proof: Orient $G$ with respect to some $2$-cut $st$. $G,H$ is not cut-sufficient, hence there is a non-compliant demand $uv$. We choose $uv$ such that $I_{uv} = \{w : u \land v \preceq w \preceq u \lor v\}$ is minimal.
By contradiction. Suppose $\mathcal{P}_{uv}$ is not covered by bubbles, there is a path $P$ that does not cross any bubble, and a central tight cut $C$ such that $|E(P) \cap \delta_G(C)| = 3$ (more than $3$ would give a $K_4$). Define $a$, $b$, $S_u$ and $S_v$ as in the following picture:
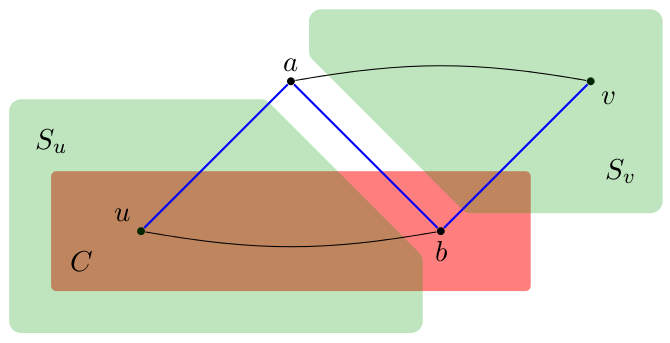
$a$ and $b$ are chosen such that the two black paths are minimal. Then there are three-disjoint ($a$,$b$)-paths, $\{a,b\}$ is a $2$-cut. Moreover, by carefully choosing $P$ and $C$, we can ensure that any $(u,b)$-path inside $C$ crosses some tight cut twice more that $P$ (a shortcut by a violating $(u,b)$-paths would decrease the number of tight cuts crosses by $P$).
$S_u$ is the component of $G \setminus \{a,b\}$ containing $u$, and $S_v$ the component containing $v$. By symmetry we may assume $s$ and $t$ are not in $S_U$. We want to show the existence of a $2$-cut $\{x,y\} \subset S_u \cup \{a,b\}$ distinct from $\{a,b\}$, and two disjoint $(x,y)$-paths, not containing $a$ or $b$, with a demand between their inner nodes. We distinguish two cases:
Suppose there is a tight cut defined by some set $S$, $u,b \notin S$, that intersects every $(u,b)$-path in $C$, but not $P$ between $u$ and $b$. Take $S$ inclusion-wise minimal. $\{a,b\}$ being a $2$-cut, $S$ does not intersect $P$ at all. Let $U$ be the component of $G[C \setminus S]$ containing $u$, and $B = C \setminus (U \cup S)$. $C \setminus U$ cannot be a bubble covering $P$, hence $\sigma(C \setminus U) > 0$. Then,
$$ \sigma(U) + \sigma(S) = \sigma(U \cup S) + 2 \sigma(U,S) \quad\text{hence}\quad \sigma(U) \geq 2\sigma(S,U)$$
$$ \sigma(U) + \sigma(C \setminus U) = \sigma(C) + 2 \sigma(U,C \setminus U) \quad\text{hence}\quad \sigma(U) < 2 \sigma(U,C \setminus U)$$
From that we get $\sigma(S,U) < \sigma(U,C \setminus U)$ and then $\sigma(S \setminus C,U) < \sigma(B,U) \leq 0$. Therefore there is a demand $pq$ with $p \in S \setminus C$ and $q \in U$. Then we prove that there is a path from $P$ to $S \cap C$ inside $S$: otherwise there would be a component $S'$ of $S$ that does not intersect $C$. Therefore $S \setminus S'$ would also cut all the $(u,b)$-paths inside $C$, and
$$ 0 = \sigma\left(S' \cup (S \setminus S')\right) = \sigma(S') + \sigma(S \setminus S') - 2 \sigma(S', S \setminus S') \geq 0$$
Hence $\sigma(S \setminus S') = 0$, contradicting the minimality of $S$. Using also the centrality of $C$, we easily get to the following situation ($a$ may be equal to $y$):
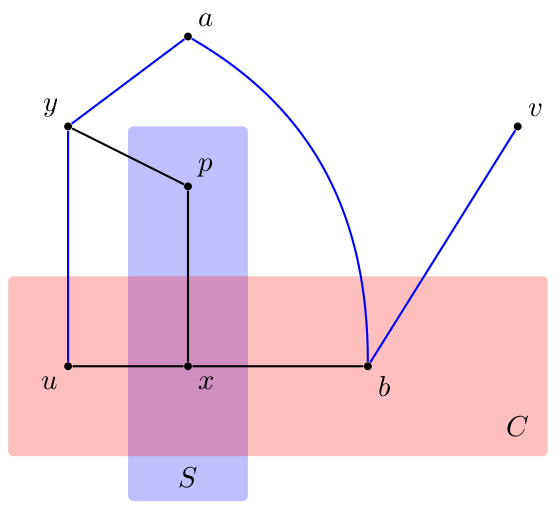
$\{x,y\}$ must be a $2$-cut because of the three disjoint $(x,y)$-paths, $u$ and $p$ must be in distinct components. Thus there must be an $(x,y)$-path containing $p$ (in the component of $u$), disjoint from the $(x,y)$-paths containing $q$.
Otherwise there is no single tight cut intersecting all the $(u,b)$-paths inside $C$. Choose a minimal family of sets defining central tight cuts that covers all such paths, without intersecting $P$ between $u$ and $b$. Then all these cuts are bubbles for $uv$. Moreover, no two of them are crossed: this would give a $K_4$, by using $P$. Also the union of them is not tight: this would give a single cut covering the $(u,b)$-paths inside $C$. Hence there must be a demand $pq$ between two of these sets. Take a $upb$ and a $uqb$ paths, using $P$ between $u$ and $b$ it is then easy to find $x,y$ with three disjoint $(x,y)$-paths, one through each of $x, y, u$.
Then in both cases $pq$ is not compliant, and $\{w : x \preceq p \land q \preceq w \preceq p \lor q \preceq y\} \subset \{w : a \preceq w \preceq b\} \subseteq I_{uv}$ (supposing wlog that $a \preceq b$), contradicting the choice of $uv$.
We can now conclude the proof of theorem 1 by exhibiting an odd-spindle minor.
Proof: Consider a demand $uv$ not covered by bubble. Let $F_{uv}$ be a minimal family of bubbles covering every $(u,v)$-paths. By centrality of the bubbles, $|F_{uv}| \geq 2$. We distinguish two cases:
$m = |F_{uv}| \geq 3$. We can assume that the bubbles are disjoint: associate to each bubble a path covered only by that bubble. If two bubbles are crossed, then we can find a path between their associated paths, and using the path associated to a third bubble we get a $K_4$. Similarly there is no edge in $G$ between two bubbles.
Now contract each bubble into a single node, as well as the components of $u$ and $V$ in $G \setminus \bigcup_{B \in F_{uv}} B$. It is easy to check this operation gives a $K_{2,m}$, with each vertex of degree $2$ defining a tight cut, and a positive demand between the vertices of degree $m$. This instance also satisfies the cut condition but does not have a routing, hence there must be an odd-spindle minor.
$|F_{uv}| = 2$, $F_{uv} = \{A,B\}$. Let $U$ be the component of $G \setminus \{A,B\}$ containing $u$, and $R$ the component containing $v$. Then:
$$ 0 \leq \sigma(A \cup R) + \sigma (B \cup R) = \sigma(A \setminus B) + \sigma(B \setminus A) + 2\sigma(U,R \cup (A \cap B))$$
If $A \cap B = \emptyset$, the RHS becomes $\sigma(A) + \sigma(B) + 2\sigma(R,U) < 0$, contradiction. Hence $A \cap B$ contains at least one vertex $x$. By centrality of $A$ and $B$ we can find two $(u,v)$-paths: $P_B$ disjoint from $A \setminus B$, and $P_A$ disjoint from $B \setminus A$, and a (minimal) path $Q_A$ from $x$ to $a \in V(P_A)$ inside $A$ and a (minimal) path $Q_B$ from $x$ to $b \in V(P_B)$ inside $B$. We deduce that there are three disjoint $(a,b)$-paths, $\{a,b\}$ is a $2$-cut. Applying Lemma 6, $A \setminus B$ and $B \setminus A$ are both central.
Contract every edge not in $\delta(A) \cup \delta(B)$, this gives a $K_{2,m}$ that satisfies the cut condition. But the cuts induced by $A$ and $B$ shows that this instance is not feasible: there is an odd-spindle again.
This concludes the proof of Theorem 1.
| 1. | , , : When the cut condition is enough: a complete characterization for multiflow problems in series-parallel networks. In: Proceedings of the 44th symposium on Theory of Computing. , 19 -- 26. (2012). |
| 2. | , , : Flow-cut gaps for integer and fractional multiflows. Journal of Combinatorial Theory, Series B. Elsevier, (2012). |