Exercice 1 : Typage (5 points)
Donner le type de chacune des valeurs f, g, h, a et b.
let f x y = ((x +. y) /. 2., sqrt (x *. y))
let g = List.map (fun (x,y) -> (-x,y+1))
let h f x = f (f x x) x
let a lst =
let f accu lst = match lst with
| [] -> accu
| head::_ -> head::accu
in
List.fold_left f [] lst
let b lst = List.rev (List.map (function [] -> [] | head::_ -> head) lst)
Solution :
x et y sont tous deux flottants à cause de l'addition et de la multiplication. Le résultat est un couple de flottants, donc
val f : float -> float -> float * float
D'abord, le type de fun (x,y) -> (-x,y+1) est clairement int * int -> int * int à cause de l'addition et du moins unaire. Ensuite, on a List.map : ('a -> 'b) -> 'a list -> 'b list, donc en appliquant le premier argument on obtient :
val g : (int * int) list -> (int * int) list
f est une fonction à (au moins) deux arguments, de même type puisqu'on l'applique avec x deux fois, et dont le résultat est de même type (puisqu'on le réapplique à f), donc f : 'a -> 'a -> 'a. On en déduit :
val h : ('a -> 'a -> 'a) -> 'a -> 'a
On commence par trouver le type de la fonction auxiliaire f. L'utilisation du match indique que son deuxième argument. L'expression pour le deuxième motif nous dit que le premier argument est une liste du même type, donc f : 'c list -> 'c list -> 'c list. Par ailleurs, nous savons que List.fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a, donc 'a = 'b = 'c list et :
val a: 'a list list -> 'a list
Le premier argument de List.map est de type 'a list -> 'a (deuxième motif) avec 'a = 'b list (premier motif). Donc lst : 'b list list list, et :
val b : 'b list list list -> 'b list list
Exercice 2 : Manipulations de listes (5 points)
Implémenter les 5 fonctions suivantes.
val sum_int_list : int list -> int
val even_position_only : 'a list -> 'a list
val contains_42 : int list -> bool
val contains_a_42_pair : int list -> bool
val rotate : 'a list -> int -> 'a list
Solution :
let sum_int_list = List.fold_left (+) 0
let rec even_position_only = function
| odd::even::others -> even::(even_position_only others)
| _ -> []
let contains_42 = List.mem 42
Les deux autres exercices sont plus subtils. Le premier consiste à décider s'il existe deux entiers de la liste dont la somme vaut 42 . Une solution semble particulièrement simple :
let contains_a_42_pair lst = List.exists (fun elt -> List.mem (42 - elt) lst) lst
car si 21 est présent en un seul exemplaire, l'algorithme répond oui en formant la paire 21 + 21 qui n'est pas valide. Une solution est de parcourir la liste, et pour chaque élément tenter de l'apparier avec un élément placé après dans la liste.
let rec contains_a_42_pair = function
| head::tail -> (List.mem (42 - head) tail) || contains_a_42_pair tail
| [] -> false
Cette solution est correcte (et est la solution attendue), mais de complexité $O(n^2)$ si $n$ est la longueur de la liste. Avec un peu d'algorithmique, on peut faire mieux. On parcourt la liste de gauche à droite, en insérant les entiers dans un dictionnaire. À chaque étape on vérifie si on peut faire une paire avec l'élément courant et un entier du dictionnaire, ce qui donne une complexité de $O(n \log n)$.
module ISet = Set.Make(struct type t = int let compare = compare end)
let contains_a_42_pair lst =
snd
(List.fold_left
(fun (set,found_42) elt -> (ISet.add elt set, found_42 || ISet.mem (42 - elt) set))
(ISet.empty,false)
lst
)
On décompose le dernier exercice comme suit. D'abord on écrit une fonction pour faire une seule rotation. Puis on écrit une fonctionnelle pour répéter une fonction plusieurs fois, qu'on utilise avec la première fonction pour résoudre l'exercice. Pour la rotation simple, comme il n'est pas très efficace de concaténer un élément en fin de liste, on garde un accumulateur, qui servira à stocker la fin de la liste en ordre inverse.
let rec single_rotate (accu,list) =
match list with
| head::tail -> (head::accu,tail)
| [] -> if accu = [] then ([],[]) else single_rotate ([],List.rev accu)
let repeat f value k = if k = 0 then value else repeat f (f value) (k-1)
let rotate list n =
let (accu,suffix) = repeat single_rotate ([],list) n in
suffix @ (List.rec accu)
Exercice 3 : Fonctionnelles (1 0 points)
On définit le type des arbres binaires ainsi :
type 'a bintree =
| Leaf
| Node of 'a bintree * 'a * 'a bintree
Chaque nœud interne porte une information, d'un type arbitraire.
Donner une fonction calculant la hauteur d'un arbre binaire:
val height : 'a bintree -> int
Solution :
let rec height = function
| Leaf -> -1
| Node (left,_,right) -> 1 + max (height left) (height right)
Écrire une fonction map pour les arbres, similaire à List.map.
# map (fun x -> x+1) (Node (Node (Leaf,3,Leaf),5,Leaf));;
- : int bintree = Node (Node (Leaf, 4, Leaf), 6, Leaf)
Solution :
let rec map f = function
| Leaf -> Leaf
| Node (left,elt,right) -> Node (map f left, f elt, map f right)
Écrire une fonction fold_infix. Elle applique une fonction à toutes les informations de l'arbre, dans l'ordre infixe.
# fold_infix (fun l e -> e::l) []
(Node (Node (Node (Leaf, 3, Leaf), 1, Node (Leaf, 5, Leaf)),
0,
Node (Node (Leaf, 4, Leaf), 2, Node (Leaf, 6, Leaf)))
);;
- : int list = [6; 2; 4; 0; 5; 1; 3]
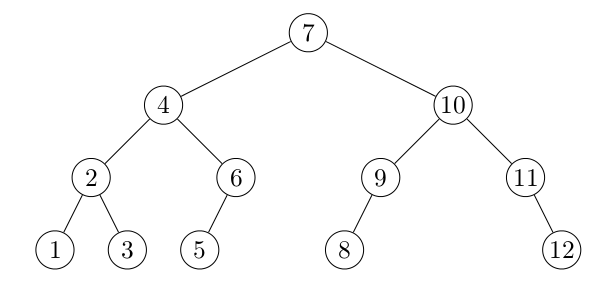
L'ordre infixe correspond à l'ordre de gauche à droite, et est illustré par la figure suivante pour laquelle les nœuds sont numérotés en ordre infixe. On doit donc appliquer la fonction d'abord aux nœuds du fils gauche de la racine, puis à la racine elle-même, puis aux nœuds du fils droit.
Solution :
let rec fold_infix f value = function
| Leaf -> value
| Node (left,elt,right) -> fold_infix f (f (fold_infix f value left) elt) right
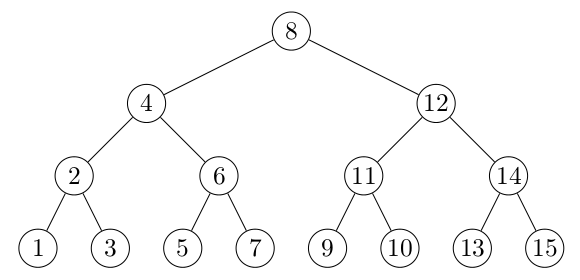
Nous souhaitons maintenant construire un arbre binaire complet de hauteur $h$, dont les informations sont les entiers de $1$ à $2^{h+1}-1$, en ordre infixe, tel que dans la figure suivante :
Nous procédons par récurrence. Le fils gauche de l'arbre de hauteur $d$ s'obtient par récurrence, et le fils droit s'obtient à partir du fils gauche par une opération arithmétique élémentaire. En déduire la fonction index_tree (vous utiliserez la fonction map définie plus tôt).
# index_tree 2;;
- : int bintree =
Node (Node (Node (Leaf, 1, Leaf), 2, Node (Leaf, 3, Leaf)),
4,
Node (Node (Leaf, 5, Leaf), 6, Node (Leaf, 7, Leaf)))
Solution :
let root = function
| Leaf -> failwith "Invalid argument (root): tree must be non-empty"
| Node (_,elt,_) -> elt
let rec index_tree = function
| 0 -> Leaf
| 1 -> Node (Leaf,1,Leaf)
| n ->
let left = index_tree (n-1) in
let top = 2 * root left in
let right = map (fun x -> x + top) left in
Node (left,top,right)
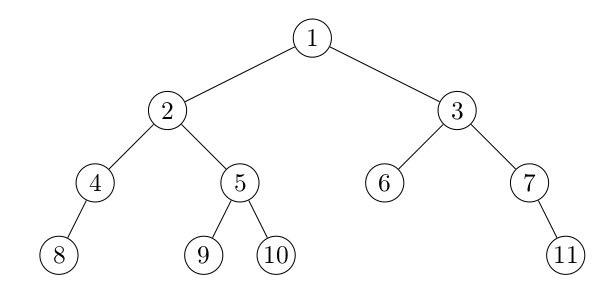
(Difficile) Écrire maintenant une autre fonction fold, qui folde maintenant par ordre de profondeur, de haut en bas puis de gauche à droite, ce qui correspond à l'ordre indiqué dans la figure suivante.
# fold (fun l e -> e::l) []
(Node (Node (Node (Leaf, 1, Leaf), 2, Node (Leaf, 3, Leaf)),
4,
Node (Node (Leaf, 5, Leaf), 6, Node (Leaf, 7, Leaf))
));;
- : int list = [7; 5; 3; 1; 6; 2; 4]
Solution :Il s'agit de faire un parcours en largeur de l'arbre depuis la racine, donc nous allons avoir besoin d'une structure de file FIFO. À chaque fois que nous examinons un nœud, on ajoute en fin de file ses deux fils. Puis on lit l'élément en tête de file. On répète tant que la file n'est pas vide.
let rec fold_by_level f init tree_queue =
match tree_queue with
| [] -> init
| Leaf::queue -> fold_by_level f init queue
| (Node (left,a,right))::queue -> fold_by_level f (f init a) (queue@[left;right])
Ici on a utilisé une file codée avec une simple liste, ce qui rend l'insertion peu efficace. On pourrait facilement réutiliser la structure de file du TD4 (donnée en fin d'énoncé) pour obtenir une meilleure complexité.
Éléments de langage
Fonctions utiles de la librairie standard :
val max : 'a -> 'a -> 'a
val sqrt : float -> float
val ( ** ) : float -> float -> float
val (@) : 'a list -> 'a list -> 'a list
Fonctions utiles du module List :
val length : 'a list -> int
val nth : 'a list -> int -> 'a
val rev : 'a list -> 'a list
val flatten : 'a list list -> 'a list
val map : ('a -> 'b) -> 'a list -> 'b list
val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a
val fold_right : ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b
val for_all : ('a -> bool) -> 'a list -> bool
val exists : ('a -> bool) -> 'a list -> bool
val mem : 'a -> 'a list -> bool
val filter : ('a -> bool) -> 'a list -> 'a list
val fast_sort : ('a -> 'a -> int) -> 'a list -> 'a list
Exemples de syntaxe :
type ratio = int * int
let rec euclid a b =
if b = 0 then a
else euclid b (a mod b)
let pgcd a b = euclid (abs a) (abs b)
let ratio p q =
let d = pgcd p q in
if q < 0 then (-p / d, q / d)
else (p/d, q/d)
let (+/) (a,b) (c,d) = ratio (a*d + b*c) (b*d)
let (++) (a,b) (c,d) = ratio (a+c) (b+d)
module Queue =
struct
type 'a t =
Queue of ('a list) * ('a list)
exception Empty
let empty = Queue ([],[])
let is_empty = function
| Queue ([],[]) -> true
| _ -> false
let queue = function
| Queue ([],l) -> Queue(List.rev l,[])
| x -> x
let snoc (Queue (l1,l2)) ele =
queue (Queue (l1,ele::l2))
let head = function
| Queue ([],_) -> raise Empty
| Queue (l,_) -> List.hd l
let tail = function
| Queue ([],_) -> raise Empty
| Queue (l1,l2) -> queue (Queue (List.tl l1,l2))
end