Exercice 1 : Le type option
Le module Pervasives fournit un type bien utile, le type option, permettant de représenter une valeur optionnelle :
type 'a option =
| None
| Some of 'a
Créez une fonction qui filtre les options d'une liste, pour garder uniquement les valeurs définies :
val concat_option : 'a option list -> 'a list
Quel est le type de la fonction suivante ?
let (>>=) opt fct = match opt with
| None -> None
| Some thing -> fct thing
Utilisez >>= pour coder une fonction prenant trois arguments de type int option, et qui renvoie une option contenant la somme des trois entiers, s'ils sont définis, ou None sinon.
Écrivez une fonction map : ('elt -> 'im) -> 'elt option ->
'im option. Proposez une version utilisant un filtrage par motif, et une version utilisant uniquement (>>=).
Écrivez une fonction find : ('elt -> bool) -> 'elt list ->
'elt option, qui calcule le premier élément d'une liste vérifiant un prédicat. find calcule une option car il se peut qu'aucun élément de la liste ne vérifie le prédicat.
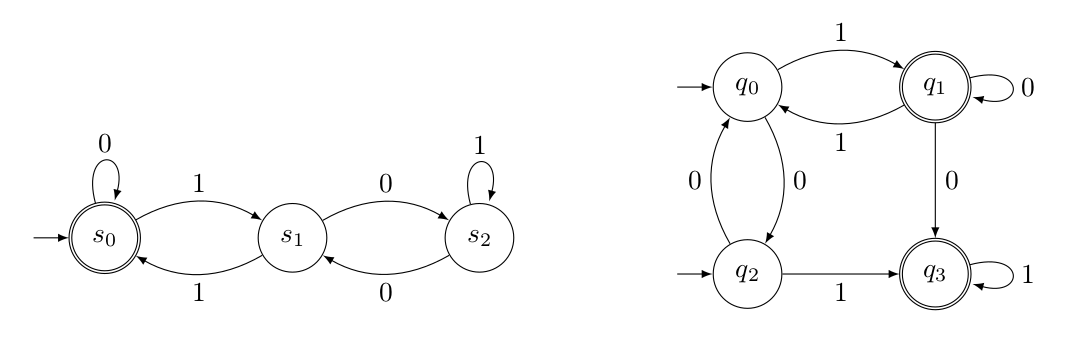
Exercice 2 : Des automates.
On souhaite réaliser l'automate de gauche.
Proposer un type pour l'alphabet du langage de l'automate de gauche.
Proposer un type pour les états de cet automate.
Définir une fonction de transition, prenant un état initial, une lettre, et retournant l'état d'arrivée.
Ajouter un prédicat déterminant si un état est final.
Définir la fonction qui prenant une liste de lettres, détermine si le mot correspondant est reconnu par l'automate.
Améliorer cette solution pour réaliser l'automate de droite. C'est plus difficile car il est non-déterministe. La fonction de transition doit donc prendre une liste d'états et retourner une liste d'états.
Exercice 3 : Nombres binaires sans chiffre '0'.
Nous allons représenter les entiers sans le chiffre '0', mais seulement avec les chiffres '1 ' et '2'. Ainsi, on peut montrer que tout nombre naturel $n$ se décompose en $n = \sum_{i=0}^k \alpha_i
2^i$, pour un certain choix de $\alpha_i \in \{1,2\}$.
Par exemple, $0 = \sum_{i=0}^{-1} 1 \cdot 2^{i}$, et $8 = 2 \cdot 2^0
+ 1 \cdot 2^1 + 1 \cdot 2^2$, etc. Étant donné que les bits ont toujours pour valeurs des puissances de 2 , on peut considérer, selon la valeur du dernier bit, qu'un entier vaut soit $1$ plus le double d'un entier, soit $2$ plus le double d'un entier, soit $0$.
Proposez un type algébrique inductif pour les entiers naturels, ainsi encodés (utilisez un cas spécial pour représenter l'entier $0$).
Écrivez une fonction succ, qui à $n$ associe $n+1$.
Programmez l'addition de deux entiers sous cette représentation.
Exercice 4 : Les listes récursivement.
Implémentez les fonctions suivantes avec des récursions et du filtrage par motifs.
val last : 'elt list -> 'elt option
val cut : int -> 'elt list -> 'elt list * 'elt list
val remove_odd_positions : 'elt list -> 'elt list
val intersperse : 'elt -> 'elt list -> 'elt list
val list_consecutive_pairs : 'elt list -> ('elt * 'elt) list
val list_suffixes : 'elt list -> 'elt list list