Nous allons définir un type des listes infinies, contenant donc une infinité de valeurs. Bien sûr, nous ne voulons pas calculer toutes les valeurs d'une liste infinie, notre temps est trop précieux. Du coup, nous allons le faire avec paresse. L'évaluation paresseuse d'une valeur consiste à ne calculer la valeur définie par une expression que si le programme en a vraiment besoin.
OCaml intègre un mécanisme pour définir des expressions paresseuses. On peut écrire :
lazy est un mot-clé permettant de construire une expression paresseuse. Il se comporte comme un constructeur du type Lazy.t.
Pour utiliser une valeur paresseuse, on peut l'observer, comme d'habitude (ou bien utiliser la fonction Lazy.force) :
(attendre deux secondes)
On constate bien avec cette exemple que l'évaluation de l'expression paresseuse est reportée au moment où on utilise son contenu.
Récupérez cette archive qui contient quelques fichiers sources fournis gracieusement.
Nous pouvons grâce à ce mécanisme d'évaluation paresseuse, créer des listes infinies. Créez un fichier colist.ml et son interface colist.mli. Nous voulons avoir à la fin cette interface :
On utilise le type :
On peut par exemple définir ainsi iterate :
Complétez le module Colist.
Le plus difficile est fait. On se propose d'utiliser les colistes pour construire des rubans, c'est-à-dire des listes bi-infinies, sans début ni fin. Pour cela, il nous faut un élément (la tête) et deux colistes (les éléments avant la tête, par convention à gauche, les éléments après la tête, par convention à droite de la tête). Les têtes des deux colistes sont alors les deux éléments voici de la tête du ruban. Avec cette représentation, il est facile de déplacer la tête vers le prochain élément vers la droite ou vers la gauche.
Créez des fichiers tape.ml et tape.mli. Ce dernier devra contenir :
Voici l'implémentation pour pp :
Quel est le type utilisé pour Tape.t ?
Complétez le module Tape.
Avec des rubans, il devient facile de faire des machines de Turing. Ce sont des automates finis disposant d'un ruban. À chaque pas de temps, la machine lit la lettre sur la tête du ruban, et choisit une transition correspondant à cette lettre. Chaque transition peut aussi écrire une lettre sur le ruban, puis déplacer le ruban d'un cran vers la gauche ou vers la droite.
Le module TuringMachine est fourni. Prenez connaissance de son interface.
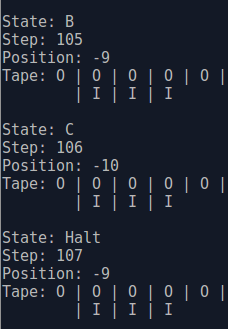
Nous voulons créer deux machines de Turing : le busy-beaver à 4 états (c'est la machine de Turing qui met le plus de temps à s'arrêter sur 4 états, avec un alphabet de deux lettres et un ruban contenant initialement uniquement la même lettre), et l'additionneur de nombres binaires.
Voici le tableau des transitions pour busy-beaver :
| État initial | Symbole lu | Symbole Écrit | Déplacement | Nouvel état |
|---|---|---|---|---|
| A | 0 | 1 | Droite | B |
| A | 1 | 1 | Gauche | B |
| B | 0 | 1 | Gauche | A |
| B | 1 | 0 | Gauche | C |
| C | 0 | 1 | Droite | Halte |
| C | 1 | 1 | Gauche | D |
| D | 0 | 1 | Droite | D |
| D | 1 | 0 | Droite | A |
Et celui pour l'additionneur
| État initial | Symbole lu | Symbole Écrit | Déplacement | Nouvel état |
|---|---|---|---|---|
| AvecRetenu | 1 | Gauche | SansRetenu | |
| AvecRetenu | 0 | Gauche | AvecRetenu | |
| AvecRetenu | 0 | Gauche | AvecRetenu | |
| AvecRetenu | 1 | Gauche | AvecRetenu | |
| SansRetenu | 0 | Gauche | SansRetenu | |
| SansRetenu | 1 | Gauche | SansRetenu | |
| SansRetenu | 1 | Gauche | SansRetenu | |
| SansRetenu | 0 | Gauche | AvecRetenu | |
| AvecRetenu | Vide | 1 | Gauche | Halte |
| SansRetenu | Vide | Vide | Gauche | Halte |
(dans tous les autres cas, écrire 0 , se déplacer à gauche et passer dans l'état Halt).
Créez deux exécutables: l'un montrant toutes les étapes de l'exécution du busy-beaver, l'autre montrant toutes les étapes de l'addition de deux entiers, où les deux entiers sont pris en argument du programme (Sys.argv.(1) : string et Sys.argv.(2) : string.
Une autre application intéressante des rubans est de créer des automates cellulaires. On peut commencer par les automates cellulaires élémentaires. Pour cela, il faudra ajouter une fonction sur les rubans, qui remplace chaque élément par le ruban dont la tête est cet élément.
On peut aussi programmer le jeu de la vie, pour cela il faut non un ruban, mais une grille infinie. On peut la représenter par un ruban (horizontal) donc chaque élément est un ruban (vertical).